
Heute vor 310 Jahren wurde der Mathematiker Leonhard Euler geboren. Ein Streitgespräch über die Existenz Gottes mit dem französischen Gelehrten Denis Diderot soll er durch diesen Satz erfolgreich beendet haben. Haben Mathematiker einen besonderen Zugang zu Gott?
Leonhard Euler gehört zu den Größten seiner Zunft. Viele mathematische Symbole, die man aus der Schule kennt, gehen auf ihn zurück: die Kreiszahl ¶, die eulersche Zahl e und die ebenso bekannte wie gefürchtete Abkürzung f(x) für Funktionen. Auch die imaginäre Einheit i, auf der die komplexen Zahlen beruhen, stammt aus seiner Feder.
1748 gelang ihm die Herleitung einer Beziehung, in der die wichtigsten Konstanten der Analysis vereint sind:
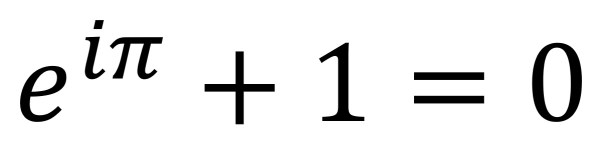
Wegen ihrer schlichten Eleganz ist sie so etwas wie die Mutter aller Formeln, die „gleichermaßen für Mystiker, Wissenschaftler, Philosophen und Mathematiker voller Deutungsmöglichkeiten“ steckt – „Vielleicht die faszinierendste Formel aller Zeiten“, wie Pierre Basieux in seinem Buch Die Top Ten der schönsten mathematischen Sätze schreibt. Etwas plakativ könnte man sagen, was Einsteins Formel E=mc2 für die Physik ist, das ist Eulers Formel für die Mathematik. Hier ist nicht der Ort, ihre Bedeutung zu erklären, aber man könnte sie in einer fernen Analogie mit einer Schauspielerin vergleichen, die so unterschiedliche Aspekte wie die Eleganz einer Audrey Hepburn, die Sinnlichkeit einer Marylin Monroe und die Unergründlichkeit einer Ingrid Bergmann perfekt und harmonisch in sich vereint (die Zuordnung der Konstanten zu den ensprechenden Damen sei dem geneigten Leser als Übung empfohlen).
Das Genie am Hofe der Zarin
Euler wurde 1707 in Basel geboren. Mit 13 Jahren besuchte er bereits Vorlesungen an der Universität, mit 16 erlangte er den Grad des Magisters und als Zwanzigjähriger wurde er als Professor an die Petersburger Akademie der Wissenschaften berufen, wo er ideale Arbeitsbedingungen vorfand. 1741 berief ihn Friedrich der Große an die Königlich-Preußische Akademie der Wissenschaften nach Berlin, wo er 25 Jahre lang blieb. Doch der Alte Fritz brachte dem Genie nicht die Wertschätzung entgegen, die dieser zweifellos verdient gehabt hätte und so kehrte Euler 1766 an den Hof Katharinas der Großen nach St. Petersburg zurück.
Zu jener Zeit soll sich das Streitgespräch mit Denis Diderot zugetragen haben. Der Franzose, ein Schriftsteller und Kunstagent der Zarin, war einer der Herausgeber der ersten großen Enzyklopädie in französischer Sprache. Ein hochgebildeter, der Aufklärung verpflichteter Mann also, der schon damals den Atheismus als die der Vernunft verpflichtete Geisteshaltung propagierte und der dem Materialismus zugeneigt war. Euler dagegen war Zeit seines Lebens gläubiger und praktizierender Protestant, der sogar eine streitbare Schrift mit dem Titel Rettung der Göttlichen Offenbarung gegen die Entwürfe der Freygeister gegen den, aus seiner Sicht unvernünftigen, Atheismus verfasst hatte.
Man kann sich gut vorstellen, wie der Literat Diderot Euler wortreich über die Irrationalität seines Glaubens aufzuklären versuchte und der Schweitzer ihn dann mit der trockenen Bemerkung „Monsieur, (a+b)n/n=x, also existiert Gott! Antworten Sie!“ sprachlos machte. Diderot soll daraufhin ausgelacht worden sein, was ihn dann letztlich zur Rückkehr nach Frankreich bewogen habe.
Wahrscheinlich hat sich die Geschichte nie so zugetragen und ob Diderot mathematisch so ungebildet war, dass er darauf hereingefallen wäre, sei dahingestellt (heutzutage hätte man bei vielen „Gebildeten“ damit eher Chancen, denke ich). Denn natürlich hätte er nur fragen müssen: „Monsieur Euler, wofür stehen die Variablen a, b, n und x in Ihrer Formel?“ und der ganze Bluff wäre in sich zusammengefallen. Niemandem muss dies klarer gewesen sein, als Euler selbst.
Existenzbeweise und ihr Tücken
Denn die Mathematik kennt zwar Existenzbeweise, aber nur innerhalb geistiger, vorher klar definierter Systeme. So konnte zum Beispiel schon Euklid beweisen, dass unendlich viele Primzahlen existieren. Das ist im Einzelfall anspruchsvoll genug und dennoch liegen die Mathematiker immer so, wie sie sich gebettet haben. Soll heißen: Sie bewegen sich in einer Welt, die sie sich selbst ausgedacht haben und in der deshalb glasklar ist, wovon man ausgehen darf und wovon nicht. Euklid wusste, dass es natürliche Zahlen, Teiler und Primzahlen gibt, weil man sich vorher darauf geeinigt hatte, was darunter zu verstehen ist. So brauchte er „nur“ seine Schlüsse zu ziehen.
In der Realität liegen die Dinge aber niemals so klar, wie im geistigen Spiel, weshalb es in den Naturwissenschaften keine rein deduktiven Beweise geben kann. Hier muss man sich erst einmal mühsam darüber verständigen, was eigentlich der Fall ist und wovon man bei einem „Beweis“ überhaupt ausgehen darf. Messfehler, Näherungen und Begriffswirrwarr sind an der Tagesordnung. In der Biologie, der Wissenschaft des Lebens, streitet man heute noch über die genaue Definition des Begriffs Leben. Von komplexeren Phänomenen wie Bewusstsein ganz zu schweigen. Und fragen Sie mal einen Physiker, was eigentlich genau Materie ist.
Schon aus diesem Grund sind mathematische Existenzbeweise, die sich auf die reale Welt beziehen, mit Vorsicht zu genießen. Und bei Fragen zur Existenz Gottes gilt dies erst recht: Wovon darf man ausgehen? Welche Eigenschaften darf man Gott zuschreiben? Bei Gott sind die Antworten so unklar, wie sie bei Primzahlen eindeutig sind. Und was bedeutet schließlich in diesem Zusammenhang überhaupt Existenz? Existiert Gott in der Art, wie eine Primzahl es tut, oder doch eher so wie ein Küchenstuhl? Oder gar beides?
Der Beethoven der Mathematik
Die Mathematik, das wird heutzutage gerne vergessen, ist eine Geisteswissenschaft und steht der Philosophie zunächst näher, als der Naturwissenschaft. Gerade bei Euler wird dies deutlich: Nachdem er schon im Alter von 33 Jahren sein rechtes Auge verloren hatte, erblindete er mit 64 vollständig. Und dennoch sollte er von nun an, blind und ganz auf seinen eigenen Geist zurückgeworfen, noch fast die Hälfte seines Lebenswerkes zu Wege bringen.
Der Mathematiker, der blind seine größten Ideen zu Papier bringt – der Vergleich mit Ludwig van Beethoven, dem Komponisten, der nach dem Verlust des Gehörsinns seine größten Werke komponierte, drängt sich auf. In diesem Sinne könnte man Euler als den Beethoven der Mathematik bezeichnen.
In die Zeit seiner Blindheit fallen auch seine Gedanken zur imaginären Einheit i, einer Zahl, die zunächst abstrus erscheint, da man mit ihr keine Größenvorstellung verbinden kann und die deshalb imaginär (als Gegensatz zu reell) genannt wird. Die Spinnerei eines erblindeten Mathematikers, so könnte man meinen.
Doch wieder einmal täuscht der erste Eindruck! Und vielleicht sind wir hier an einem Punkt angelangt, der Euler und viele Mathematiker an etwas „Höheres“ glauben lässt. Die imaginäre Einheit und die auf ihr aufgebauten komplexen Zahlen, erwiesen sich als sehr nützlich zur Beschreibung realer Phänomene. So sind die komplexen Zahlen, neben zahlreichen anderen Anwendungen, elementar für die Formulierung der Quantenmechanik, einer der erfolgreichsten naturwissenschaftlichen Theorien überhaupt. Wie so oft ist das Geistige eine perfekte, idealisierte Beschreibung des Realen. Warum sich dies so verhält, ist bis heute ein ungelöstes Rätsel. Und so ist es für Mathematiker nicht so abwegig zu glauben, dass das Geistige in irgendeiner Form tatsächlich existiert und das Reale nur sein Abbild ist – ganz im Sinne von Platon.
Leonhard Euler starb 1783 im Alter von 76 Jahren in St. Petersburg.


Naturwissenschaftler und Mathematiker könnten viele ihre noch ungelösten Fragen, durch ein (vertieftes) Zen-Buddhistische Studium er-klären und erweitern bzw darauf insperierende Antworten finden.
LikeGefällt 2 Personen
„Soll heißen: Sie (die Mathematiker) bewegen sich in einer Welt, die sie sich selbst ausgedacht haben und in der deshalb glasklar ist, wovon man ausgehen darf und wovon nicht.“
-> „ausgedacht“ beschreibt nicht vollständig, warum . . . ..
„Und so ist es für Mathematiker nicht so abwegig zu glauben, dass das Geistige in irgendeiner Form tatsächlich existiert und das Reale nur sein Abbild ist – ganz im Sinne von Platon.“
-> finden wir auch Antworten in unserer Zeit? Besser noch Instrumente, welche uns ermöglichen die Realität von vor 400 Jahren (30 jähriger Krieg), von vor 100 Jahren (Große Sozialistische Oktoberrevolution) nicht zu wiederholen? Das Geistige in einen Griff zu bekommen, welche ein militärisches Eingreifen im Sinne Carl Philipp Gottlieb von Clausewitz nicht notwendig machen würde: Die Achse von Zweck, Ziel und Mittel · „Der Krieg ist eine bloße Fortsetzung der Politik mit anderen Mitteln.“ Kann eine Politik eine Strategie und Taktik besitzen, welche das Geistige formt und das Reale menschenwürdig abbilden kann? Aus meiner Sicht kann Mathematik verknüpft mit Zeit solches bewirken . . . .. mein Gott (verblüffter Ausruf): Jetzt suche ich meine Antworten in noch viel älteren Zeiten: in den Anfängen des Universums . . . .. und auch dies ist ziemlich ungenau formuliert: ich suche meine Antworten in einer „Gleichzeitigkeit“ (nicht nur im Jetzt!) . . . .. in einem Zustand, in dem Alt und Jung sich noch nicht voneinander getrennt haben . . . .. und ich habe mir das nicht selbst ausgedacht, wie oben es die Mathematiker tun (sollen) . . . .. 🙂
LikeLike
Ein kleines Gedicht zur Mathematik:
MATHEMATIKER
Die Mathematik erfordert Wissen,
Doch nicht als ewiges Ruhekissen.
Für die mathematischen Prozesse
Braucht es Geist und Akkuratesse.
Man erwartet wegweisende Ideen,
Mathematiker müssen vorangeh’n.
Sie lieben Summen und Differenzen
Genauso wie Wurzeln und Potenzen.
Vektorrechnung und Trigonometrie,
Wie auch die Algebra begeistern sie.
Differential, Integral – ganz egal,
Sie beherrschen Infinitesimal.
Sie quadrieren und interpolieren,
Wollen ständig mit Zahlen jonglieren.
Sie steh’n auf Euklid und Pythagoras,
Haben an Logarithmen großen Spaß.
Sie bearbeiten Funktionen versiert,
Die Kurvendiskussion wird geführt.
Extremwerte sind gar kein Problem,
Sie lösen jedes Gleichungssystem.
Sie führen die kniffligsten Beweise,
Berechnen flott Trapeze und Kreise.
Das alles ohne den geringsten Frust,
Mathematik ist ihnen eine Lust.
Rainer Kirmse , Altenburg
Herzliche Grüße aus Thüringen
LikeLike
Ein etwas unorthodoxes
Gedicht zum Allgemeinwissen:
WISSEN FÜR BESSERWISSER
Es hält unser Blut in Fluss der
Thrombozytenaggregationshemmer,
Welch klangvolles Wort.
Bandar Seri Begawan ist
Hauptstadt von Brunei,
Ein herrlicher Ort.
Kalaallit Nunaat ist Grönland,
Der Mount Godwin-Austen
Auch als K 2 bekannt,
Eyjafjallajökull ein Vulkan
Im vulkanreichen Island.
Vigdis Finnbogadottir
War mal Präsidentin hier.
Wir kennen Parallaxensekunde
Und Desoxyribonukleinsäure gut,
Zaubern noch mit links die
Positronenemissionstomografie
Aus dem Hut.
Die Stadt Hodmezövásárhely
Fordert schon etwas Mut.
Spricht man diese Worte
Zügig und unfallfrei aus,
Erntet man sicher Applaus.
Kann man sie noch deuten,
Ist man wohl unheimlich
Den Leuten.
Rainer Kirmse , Altenburg
Herzliche Grüße aus der Skatstadt
LikeLike
Mathematik findet Anwendung nur im Raumzeit-Gefilde. Darüber hinaus bleibt sie unbrauchbar. Für das Unermessliche ist selbst die edelste Logik nur ein armer Witz.
LikeLike
Mathematik ist weit mehr als Logik, sie ist eine Geisteswissenschaft. Gerade sie ermöglicht es uns, uns an das „Unermessliche“ heranzutasten.
LikeLike
Geisteswissenschaft ja, doch nicht mehr als Logik. Sie ermöglicht dem limitierten Verstande keineswegs sich an das Unermessliche heranzutasten, sondern nur davor im Zahlenkreise zu herumzuirren.
LikeLike
In der Mathematik können wir verschiedene Arten von Unendlichkeiten erfassen und vergleichen, uns in Räumen mit beliebig vielen Dimensionen bewegen und uns ins Reich der imaginären Zahlen (siehe Artikel) begeben.
Natürlich kann Mathematik nicht alles (auch dazu: siehe Artikel). Aber verzeih die Frage: Könnte es sein, dass Deine Kenntnisse über Mathematik nicht so umfassend sind? Die Behauptung, Mathematik sei nicht mehr als Logik, legt diese Vermutung nahe.
LikeLike
Was kann Mathematik sein außer Logik?
Gefühl?
Es bewegt sich nur innerhalb von Zeit und Raum. Mehr nicht.
Tick- Zeit; Tack- Raum.
Es ist das limitierte Denken. Nicht mehr, nicht weniger.
Verzeihe mir auch die Frage: könnte sein, dass du nur denken kannst?
LikeLike
Mathematik erfasst Unendlichkeit nicht.
„Unendlichkeiten “ gibt es nicht.
Ohne Mathematik bewegt sich kaum was im Alltag, jedoch auch das ist nicht alles. Das unsichtbare „Unmathematische“ wird zu sichtbarem „Mathematischen“, das die Logik erfassen und verarbeiten kann.
Das Unlogische und Unvorstellbare, das der Logik Jenseitige läßt die Logik nur seinen Bademantel sehen. Das Nackte bleibt dem Auge der Logik stets verborgen.
Mathematik erleichtert zwar teilweise den Zweck materiellen Lebens, das immer weit mehr als Formeln und Zahlen bedeutet. Alleine das einzige Gefühl der Liebe kann Mathematik weder erfassen, noch beweisen und widersprechen. Da bleibt sie nur ein Dampf, den das besessene Logik- Ego verherrlicht.
LikeLike
„Was kann Mathematik sein außer Logik?“
Imagination, Kreativität und Phantasie
„Verzeihe mir auch die Frage: könnte sein, dass du nur denken kannst?“
Nein.
LikeLike
Das ist Mathematik:
LikeLike
Im Video sehe ich „Physik“! – Nur Physik. Der Mensch empfindet mittels Physik. Jeder Buchstabe auf der Tafel, Papier oder Bildschirm ist Physik.
Jede Ziffer, jede Zahl benötigt Energie, welche verschiedene Formen annehmen muss, um „Ein Denken“ anzustoßen und in Bewegung zu bringen. Warum eigentlich?
Um auf „Ein Unermessbarem“ zu surfen und dem Selbst in seiner Zeit – Raum empfinden zu lassen. Es gilt sicherlich dem Unermessbarem verstehen zu geben, was es auch sein kann . . . ..
Nur muss das Selbst bereit sein, sein Sein im Unermessbarem aufzulösen. Dies gelingt nur, wenn das Unermessbare bereit ist, sich selbst zu verstehen . . . .. dann verschmelzen beide Sein zu dem, aus welchem sie gegründet wurden . . . ..
LikeLike
„Im Video sehe ich „Physik“! – Nur Physik.“
Nein, da irrst Du Dich. Das Video zeigt reine Mathematik. Auf der komplexen Zahlenebene wird eine Funktion iteriert, also immer wieder von neuem auf jede komplexe Zahl angewendet. Dann schaut man ob der Wert jeweils gegen unendlich geht oder nicht und färbt die jeweilige Zahl, die ja einem Punkt in der Ebene entspricht, entsprechend ein. Dabei ensteht dieses unglaubliche Muster, das sich beliebig vergrößern lässt.
Wie gesagt – reine Mathematik.
LikeLike
Du betrachtest also auch aneinander gereihte Punkte mit verschiedenen Farben! Und du nennst dies „reine Mathematik“.
Einen Algorithmus, welcher diese schönen Muster auf meinen Bildschirm „zaubert“, sehe ich nicht.
Ich irre mich nicht.
LikeLike
Nein, den Algorithmus sieht man nicht, das ist richtig. Deswegen habe ich versucht ihn kurz zu erklären.
Man sieht ja auch den Maler nicht, wenn man sein Bild anschaut.
LikeLike
Hier nochmal erklärt. Wie gesagt, alles Mathematik.
LikeLike
Nur noch einmal zur Erinnerung: „Haben Mathematiker einen besonderen Zugang zu Gott?“
Auch ein sehr schönes Video. Kein Mathematiker kann ohne Physik Mathematik bildlich darstellen. Die Punkte und Linien auf dem Bildschirm werden durch den Computer sichtbar gemacht. Wenn ich 1 x 1 = 1 darstelle, ist das nicht die Mathematik selbst, sondern eine symbolhafte Darstellung mittels der Physik. Die reine Mathematik, wie du sie nennst, versteckt sich hinter dieser materiellen Hülle.
Mathematik ist etwas Unermessliches. Mir gefällt dieser Begriff, weil in ihm das Wort „messen“ steckt. Der Mathematiker erschafft Symbole, Ziffern, Regeln und wird durch Physik genötigt Symbole, Ziffern, Regeln materiell darzustellen. Er kann als einzelner Mensch aus dem Unermesslichem der Mathematik zwar schöpfen, aber ohne Physik nicht festhalten, was er gerade erlebt hat.
Mathematik ist reiner Geist.
Physik ist reine Natur.
LikeLike
Der Verstand versteht nicht mal sich selbst, geschweige denn Zeit und Raum. Seine Nahrung besteht nur aus Gedanken, Zahlen und Regeln. Nun, das ist nicht falsch, sondern völlig natürlich, es entspricht seiner limitierten Natur.
N.B. Er kann weder mathematisch, noch philosophisch die „0“ und das Infinituum erfassen.
Warum?
Weil mit einem Pappbecher den Ozean nicht messen kann.
LikeLike